Mathematics
We believe that the learning of mathematics at Ladypool should be outstanding for all children. Maths should be fun, engaging and inspire children to become confident mathematicians who are well-equipped to apply their skills in everyday life.
Intent
At Ladypool Primary School, our intention is that children share a love of mathematical learning, whatever their ability or starting place. We aim to ensure that they are able to confidently use and apply mathematical concepts across a variety of situations. We also expect children to clearly articulate their ideas, thoughts and reasoning processes, enabling deeper learning. We encourage a resilient attitude in Maths where children make mistakes, analyse them and learn from them, justifying and explaining as they do this.
We provide all pupils with direct teaching every day, which is oral, interactive and stimulating. Teaching styles and lesson structure provide opportunities for pupils to consolidate their previous learning, use and apply their knowledge, understanding and skills, pose and ask questions, investigate mathematical ideas, reflect on their own learning and make links with other work. A typical lesson will comprise of an anchor task that hooks the children into learning, a 'Get ready' section to apply prior knowledge, direct teaching of new or consolidated content followed by independent work. When teaching content, the sequence followed is 'I do, we do. you do'.
Implementation
At Ladypool, we follow the mastery approach using the White Rose Maths schemes of learning alongside Mastering the Curriculum and Primary Stars. Mastery teaching allows our children to acquire a deep and transferable understanding of mathematical concepts that are tailored and inclusive. We use a range of resources to enable our teachers to select the most appropriate to teach each concept and for our children to experience different question types and apply their learning to different scenarios. A mathematical concept or skill has been mastered when a child can show it in multiple ways, using the mathematical language to explain their ideas, and can independently apply the concept to new problems in unfamiliar situations.
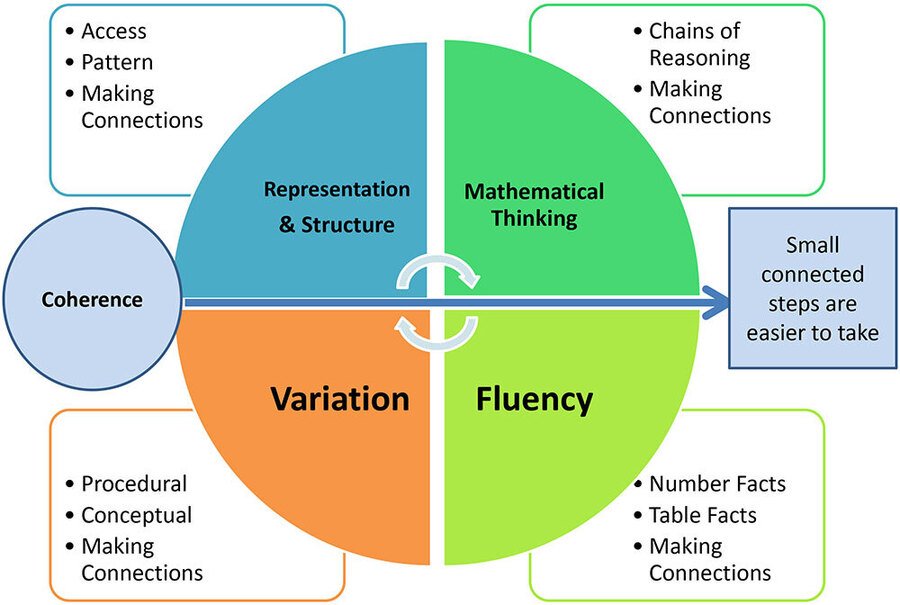
Fluency: embedding mathematical practices that involve knowing key mathematical facts and being able to recall them quickly and accurately.

Reasoning: is the process of applying logical thinking to a situation to derive the correct problem solving strategy for a given question, and using this method to develop and describe a solution.

Problem solving: is finding a way to apply the knowledge and skills you have to answer unfamiliar types of problems.

Impact
Children should:
- have a good understanding of mathematical concepts including the 4 operations
- be able to clearly explain their reasoning and justify their thought processes
- have quick recall of number facts at an age related level
- be able to flexibly move between different contexts and representations of mathematics
- have the ability to recognise relationships and make connections in mathematics
- make cross curricular links
- be happy, confident, articulate and well rounded learners with a growing passion for learning













